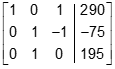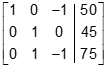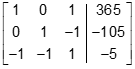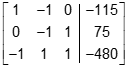Study Guide

Field 211: Advanced Mathematics 
Sample Selected-Response Questions

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

Expand All | Collapse All

General Test Directions

This test contains two sections: (1) a section with selected-response questions and (2) a constructed-response section. The directions for the constructed-response assignment appear before that section.

Each question in the first section is a selected-response question with four answer choices. Read each question and answer choice carefully and choose the  start uppercase ONE end uppercase  best answer. Try to answer all questions. In general, if you have some knowledge about a question, it is better to try to answer it. You will  start uppercase NOT end uppercase  be penalized for guessing.

A calculator is available to you for this test. To access the calculator, click on the calculator icon located in the upper left corner of the screen. A pop-up window containing the calculator will appear. You can reposition the calculator by placing your cursor in the blue area above the calculator and dragging the window to the location of your choice.

Use the numbers on the keyboard and/or point and click with the mouse to enter your computations into the on-screen calculator. When you are finished, close the calculator by clicking the close calculator icon button in the upper right corner of the calculator.

Reference materials will also be available to you during this test. To access these reference materials, click on the reference materials icon located in the lower left corner of the screen.

You may work on and complete the selected-response questions and the constructed-response assignment in any order that you choose. Be sure to allocate your time carefully so that you are able to complete the entire test within the testing session.

Use of any other type of calculator or outside reference materials during the testing session is prohibited.

Sample Selected-Response Questions

Competency 0001 
Apply knowledge of the structure, properties, and operations of the real number system.

1.  start bold Use the diagram below to answer the question that follows. end bold 

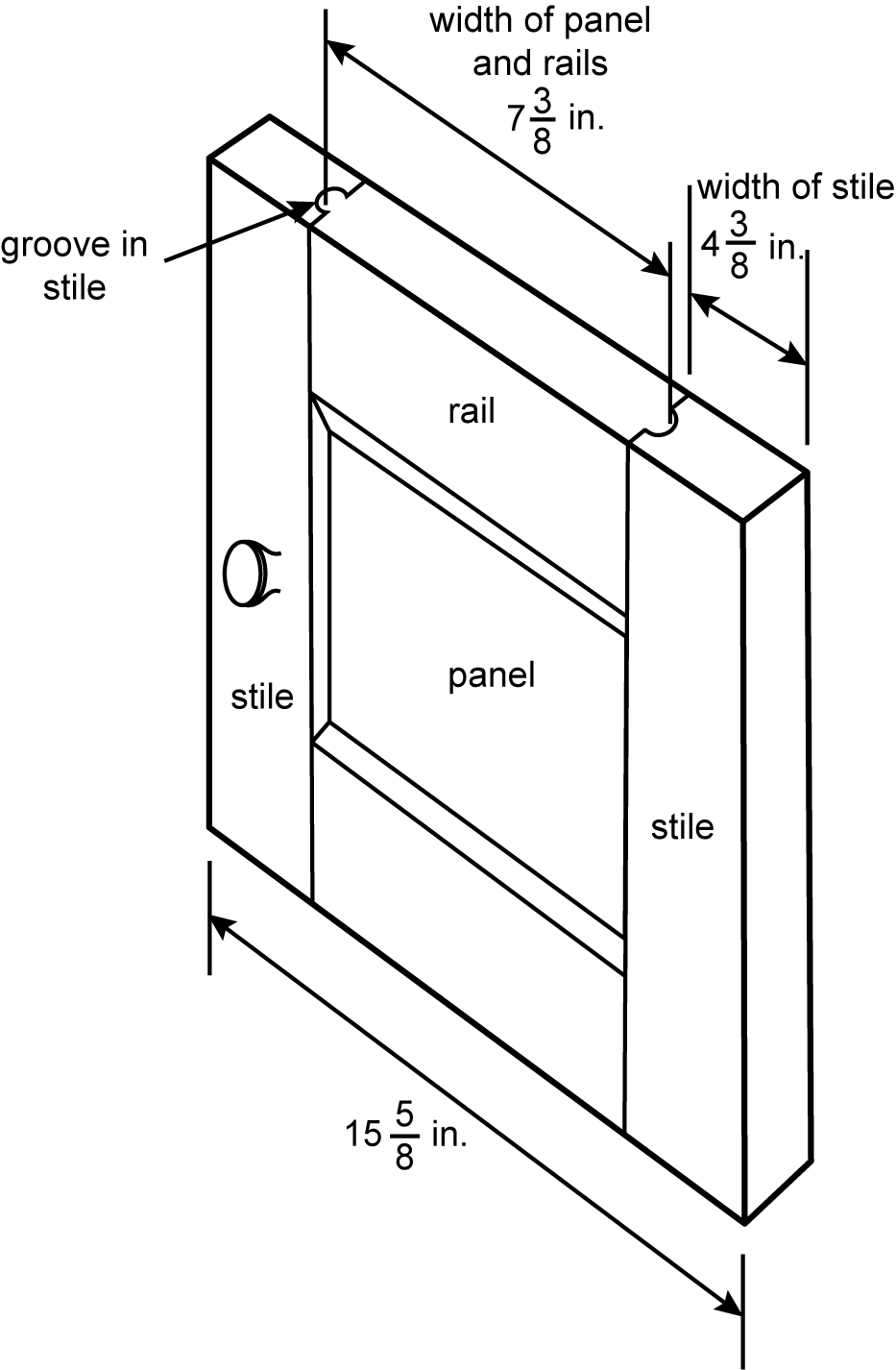
a diagram of a cabinet door blueprint

An image of a cabinet door. The cabinet door consists of three pieces of wood attached to form a row of three sections. The center piece of the cabinet is labeled panel and has a width of seven and three eighths inches. The two pieces on the left and right of the center panel are labeled stiles. Each stile is labeled four and three eighths inches. The stiles each have a groove carved out of them that the center panel fits into, such that when the pieces are assembled, the widths of the two stiles each overlap with the width of the center panel by a small unknown amount. The total width of the assembled stiles and panel is fifteen and five eighths inches.

A carpenter is building a cabinet door. The door will have two vertical stiles that are  4 and 3 eighths  inches wide, a panel that is  7 and 3 eighths  inches wide, and a total width of  15 and 5 eighths  inches. A middle section, comprising horizontal rails and a panel, will be added between the two stiles. Each stile has a groove cut into it that the middle section will slot into. What is the maximum depth of the grooves?

  1.  1 sixteenth  inch
  2.  1 eighth  inch
  3.  1 fourth  inch
  4.  1 half  inch

Correct Response: C. The total width of the cabinet door can be expressed two ways. One is the given total width of the cabinet door, 15 and 5 eighths. The other is the sum of the widths of the three pieces minus the combined depth of the two grooves. Letting x equal the maximum depth of a groove, this yields the expression 7 and 3 eighths plus 4 and 3 eighths plus 4 and 3 eighths minus 2 x. Setting the two ways of expressing the total width equal to each other yields the equation 15 and 5 eighths equals 7 and 3 eighths plus 4 and 3 eighths plus 4 and 3 eighths minus 2 x. Solving this equation shows that x, the maximum depth of a groove, equals 1 fourth inch.

Competency 0002 
Apply knowledge of number theory and the complex number system.

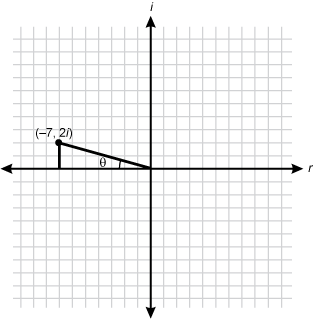
2. The point  z equals negative 7 plus 2 times i  is rotated clockwise about the origin of a complex plane so that it rests on the positive real axis. Which of the following values best represents the angle of the rotation?

  1.  0 point 2 7 8 3  radians
  2.  1 point 2 9 2 5  radians
  3.  2 point 8 6 3 3  radians
  4.  3 point 4 1 9 9  radians

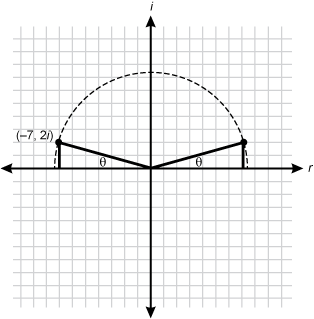
Correct Response: C. When graphed on a coordinate plane, point z can be visualized as being a vertex of a right triangle as shown. A coordinate plane with the y axis representing the complex part of a number and the x axis representing the real part of a number is shown. The point negative seven comma two i is graphed on the plane. A vertical segment is drawn between the point and the x axis. A diagonal segment is drawn from the point to the origin. The angle between the x axis and the diagonal segment is labeled theta. Reflecting the right triangle over the y-axis and drawing the path of point z’s rotation creates the drawing shown below. A coordinate plane with the y axis representing the complex part of a number and the x axis representing the real part of a number is shown. The point negative seven comma two i is graphed on the plane. A vertical segment is drawn between the point and the x axis. A diagonal segment is drawn from the point to the origin. The angle between the x axis and the diagonal segment is labeled theta. The reflection of the point across the y axis is shown. The reflected point also has a vertical segment drawn between it and the x axis and a diagonal segment drawn from the reflected point to the origin. The angle between the diagonal segment drawn from the reflected point and the x axis is labeled theta. A dotted semi-circle passes through the point and the reflected point before reaching the x axis on either side of the graph. The angle of rotation can therefore be thought of as pi minus theta. The measure of theta can be found using right-angle trigonometry: tangent of theta equals 2 sevenths, therefore theta equals inverse tangent of 2 sevenths which approximately equals 0 point 2 7 8 3. The equation pi minus theta is therefore approximately 2 point 8 6 3 3 radians.

Competency 0004 
Analyze the principles and properties of linear algebra.

3. A city planner investigates the flow of traffic through a network of one-way streets that intersect in three places. They measure the rate (in vehicles per hour) at which cars move through several sections of the road and label a map with each rate accompanied by an arrow to show the direction of travel for the traffic in each street segment as seen below.

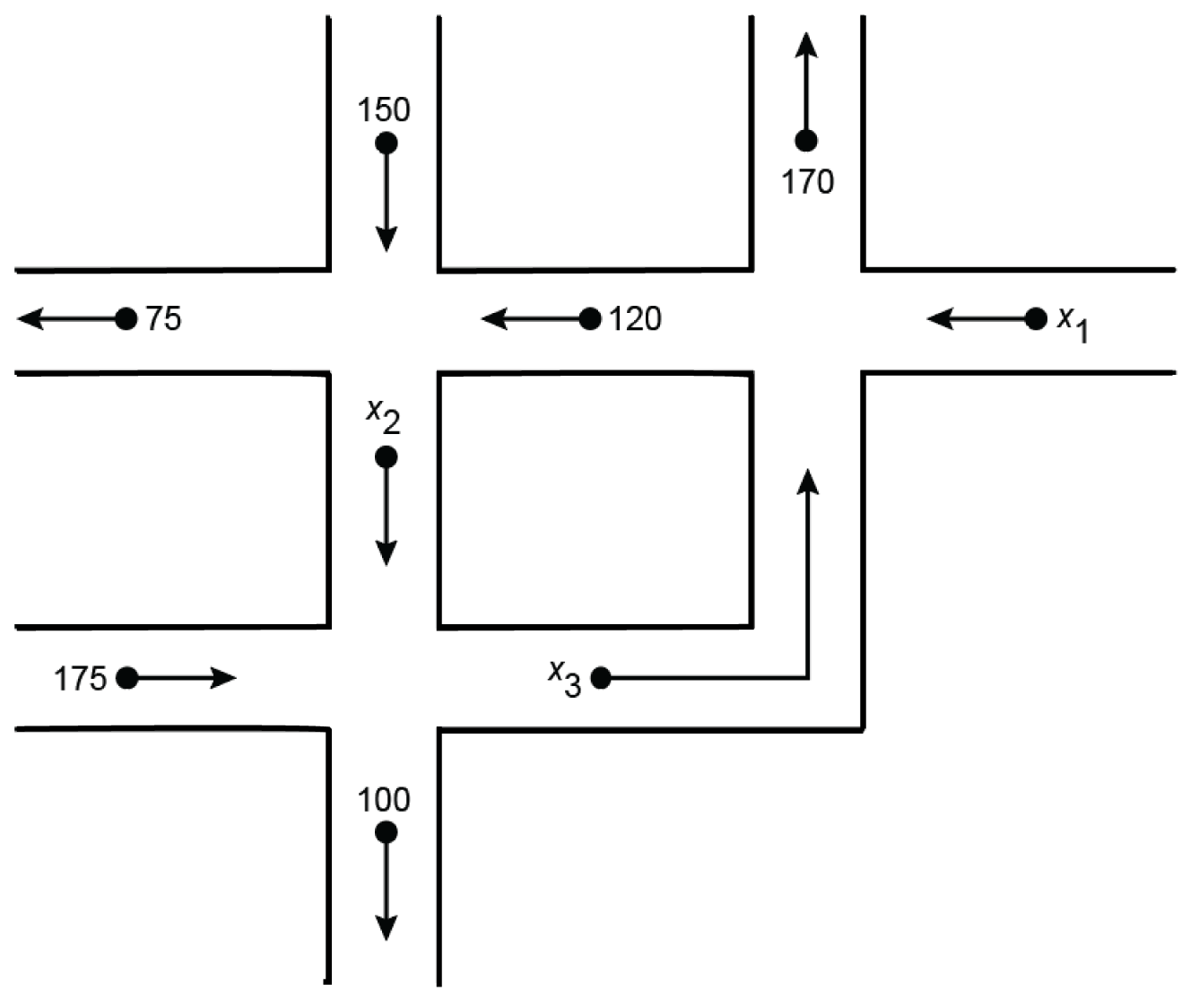
a diagram of a map of the intersections of multiple streets

A map of the intersections of multiple streets. Each intersection is labeled with the net rate (in cars per minute, or c p m ) that enter or exit the intersection from each direction. The first intersection is labeled with one hundred and fifty c p m entering from the north, one hundred and twenty c p m entering from the east, x sub two c p m exiting to the south, and seventy five c p m exiting to the west. The second intersection is labeled with one hundred and seventy c p m exiting to the north, x sub one c p m entering from the east, x sub three c p m entering from the south, and one hundred and twenty c p m exiting to the west. The third intersection is labeled with x sub two c p m entering from the north, x sub three c p m exiting to the east, one hundred c p m exiting to the south, and one hundred and seventy five c p m entering from the west.

Which of the following matrices can be used to determine the rates, in vehicles per minute, of traffic represented by the labels  x sub 1 ,  x sub 2 , and  x sub 3 ?

  1.  A three by four matrix is shown with a line segment between the third and fourth columns. The first row reads, from left to right, one, zero, one, two hundred and ninety. The second row reads, from left to right, zero, one, negative one, negative seventy five. The third row reads, from left to right, zero, one, zero, one hundred and ninety five. 
  2.  A three by four matrix is shown with a line segment between the third and fourth columns. The first row reads, from left to right, one, zero, negative one, fifty. The second row reads, from left to right, zero, one, zero, forty five. The third row reads, from left to right, zero, one, negative one, seventy five. 
  3.  A three by four matrix is shown with a line segment between the third and fourth columns. The first row reads, from left to right, one, zero, one, three hundred and sixty five. The second row reads, from left to right, zero, one, negative one, negative one hundred and five. The third row reads, from left to right, negative one, negative one, one, negative five. 
  4.  A three by four matrix is shown with a line segment between the third and fourth columns. The first row reads, from left to right, one, negative one, zero, negative one hundred and fifteen. The second row reads, from left to right, zero, negative one, one, seventy five. The third row reads, from left to right, negative one, one, one, negative four hundred and eighty. 

Correct Response: A. Each intersection in the diagram must have an equal number of cars entering and cars exiting. This leads to the equations x sub 1 plus x sub 3 equals 120 plus 170, x sub 2 plus 175 equals 100 plus x sub 3, and 120 plus 150 equals 75 plus x sub 2. Rearranging these equations yields the equations x sub 1 plus x sub 3 equals 290, x sub 2 plus x sub 3 equals negative 75, and x sub 2 equals 215. Writing this system of equations as an augmented matrix results in the matrix shown in response A.

Competency 0006 
Analyze the properties of quadratic and higher-order polynomial expressions, relations, and functions.

4. A quadratic function is written in the form  f of x equals a times x squared plus b times x plus c , where a, b, and c are integers. The y-coordinate of this function's vertex is the rational number t. The table shown below is made using this function.

table displaying the results of a function
x y
 negative 1   t minus 12 point 5 
0  t minus 4 point 5 
1  t minus 0 point 5 
 1 point 5  t
2  t minus 0 point 5 
3  t minus 4 point 5 
4  t minus 12 point 5 

Which of the following pairs of expressions could describe the coefficients a and b of function  f of x ?

  1. a  equals  2, b =  negative 6
  2. a  equals   negative 2, b = 6
  3. a  equals   negative 1, b =  negative 3
  4. a  equals  1, b =  negative 3

Correct Response: B. The table shows that the y-value is the same for the x-values 1 and 2. This means the vertex is exactly halfway between these two points or at x = 1 point 5. As the input x-values increase or decrease from 1 point 5, the y-values decrease. This indicates that the parabola the function describes opens downward. This implies that the a coefficient must be negative. Since the vertex is to the right of the y-axis, and the parabola faces down, the b coefficient must be positive. The only response that has a negative a and positive b is response B.

Competency 0008 
Apply the principles and properties of exponential and logarithmic expressions and functions.

5.  start bold Use the information below to answer the question that follows. end bold 

The equation  T of t equals T sub s plus D naught times e to the quantity negative 0 point 0 2 times t  models the temperature of a particular volume of milk that is cooling after it has been warmed where:

Note: All times are in minutes, and all temperatures are in degrees Fahrenheit.

As part of a process to make yogurt, a person pours a container of milk into a pot and heats it over a stovetop to 180 degrees Fahrenheit . Later, the person sets the pot on a countertop in a kitchen that is 70 degrees Fahrenheit  and waits for it to cool to a temperature range of 108 degrees Fahrenheit  to 112 degrees Fahrenheit , at which point they add yogurt starter to the milk. If the above equation effectively models the temperature of the milk as it cools, how long does it predict that the person must wait before they add the yogurt starter to the milk?

  1. 20 minutes
  2. 30 minutes
  3. 40 minutes
  4. 50 minutes

Correct Response: D. T of t is the temperature at a given time t. Since the person waits for the temperature to be between 108 degrees Fahrenheit and 112 degrees Fahrenheit, estimate that T of t equals 110 degrees Fahrenheit. Then, the given formula with the appropriate values substituted becomes 110 equals 70 plus 110 times e to the quantity negative 0 point 0 2 times t. To solve this equation, subtract 70 from each side of the equation, then divide each side of the equation by 110 to obtain 40 over 110 equals e to the quantity negative 0 point 0 2 times t. Next, take the natural logarithm of each side to obtain the natural log of the fraction 40 over 110 equals negative 0 point 0 2 times t. Simplify the logarithm to obtain negative 1 point 0 1 1 6 equals negative 0 point 0 2 times t, then divide each side by negative 0 point 0 2 to obtain t equals 50 point 5 8, which is closest to response D.

Competency 0010 
Apply the principles and techniques of trigonometry to model and solve problems.

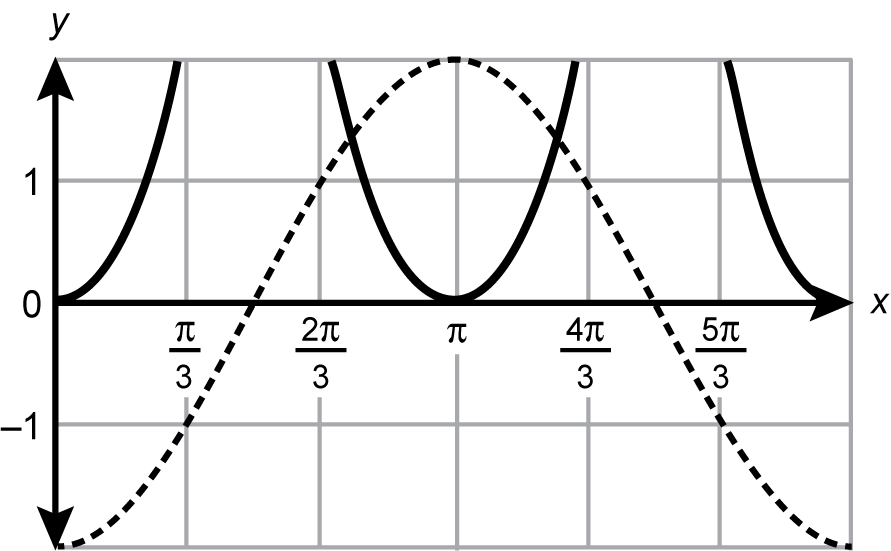
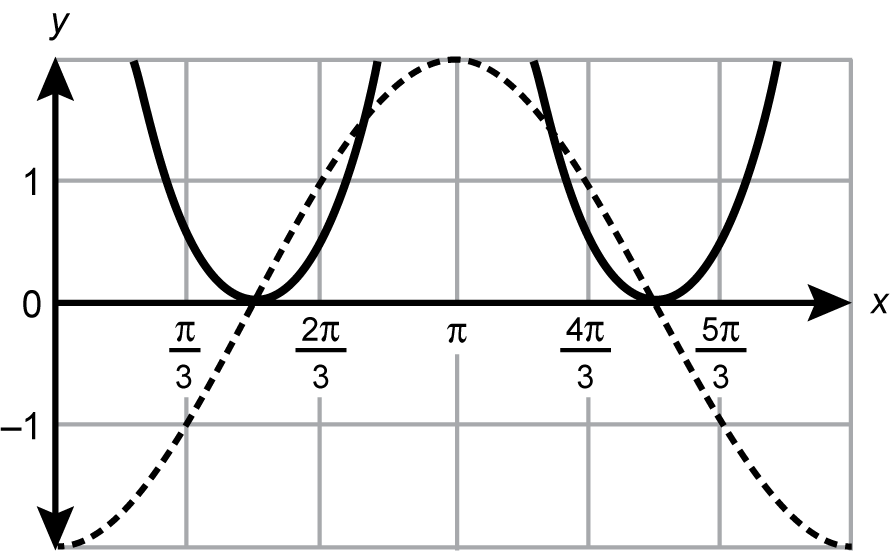
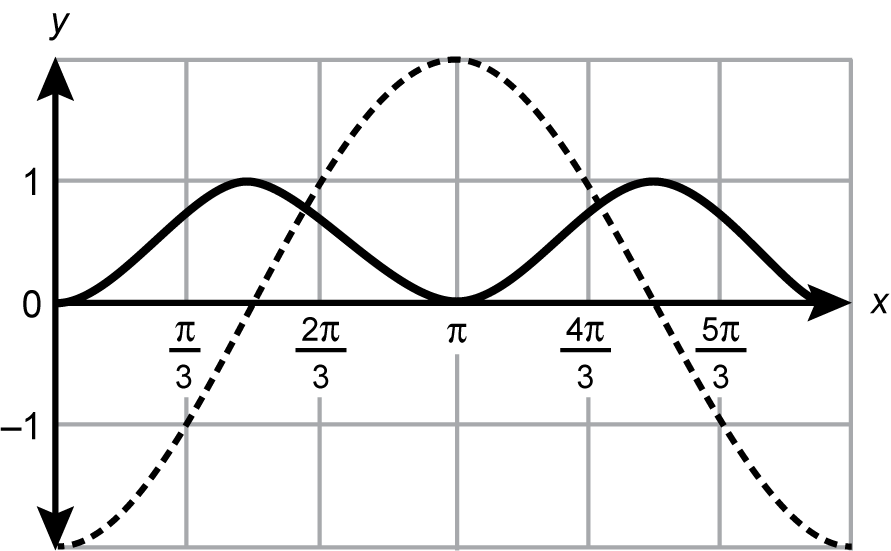
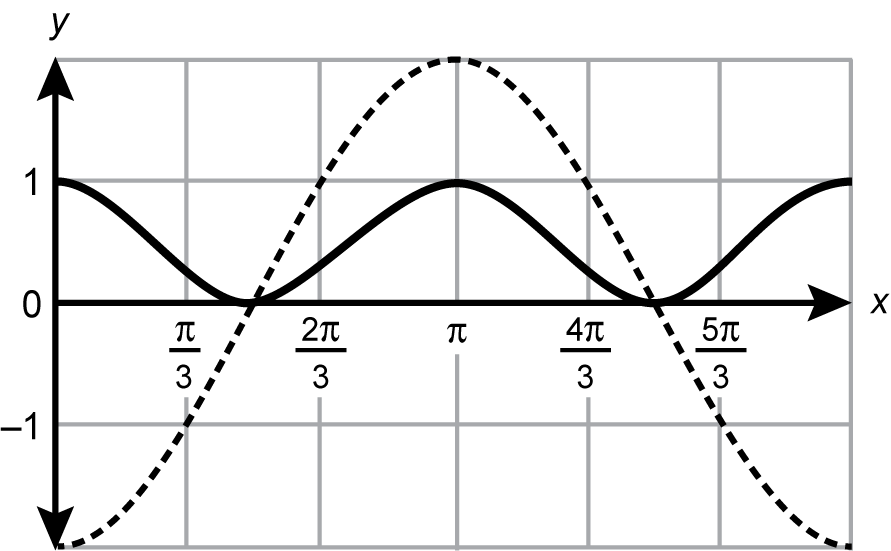
6. The solutions to the equation  negative 2 times cosine of x times cotangent squared of x equals 1  within the interval  0 is less than or equal to x which is less than or equal to 2 times pi  can be found graphically by multiplying both sides of the equation by the reciprocal of  cotangent squared of x  and plotting the functions that result on each side of the equation. Which of the following graphs does this method generate?

  1.  A coordinate plane is shown with tick marks along the y axis at intervals of one from negative two to two and with tick marks along the x axis at intervals of pi over three from zero to two pi. A curve drawn with a dotted line starts at the point 0 comma negative two, passes through three pi over six comma zero, reaches a maximum at the point pi comma two, then changes direction to pass through the point nine pi over six comma zero followed by the point two pi comma negative two. A curve drawn with a solid line starts at the point zero comma zero, then continues upward until it leaves the top of the graph at approximately pi over three comma two. It returns to the top of the graph at approximately two pi over three comma two and continues down to the point pi comma 0 before changing direction to exit out of the graph at approximately four pi over three comma two. The curve returns to the graph at approximately five pi over three comma two and continues to the point two pi comma zero. 
  2.  A coordinate plane is shown with tick marks along the y axis at intervals of one from negative two to two and with tick marks along the x axis at intervals of pi over three from zero to two pi. A curve drawn with a dotted line starts at the point zero comma negative two, passes through three pi over six comma zero, reaches a maximum at the point pi comma two, then changes direction to pass through the point nine pi over six comma zero followed by the point two pi comma negative two. A curve drawn with a solid line starts at approximately pi over six comma two, continues to approximately three pi over six comma zero, then continues upward to exit the graph at approximately five pi over six comma two. It returns to the graph at approximately seven pi over six comma two, passes through nine pi over six comma zero, and exits the graph again at approximately eleven pi over six comma two. 
  3.  A coordinate plane is shown with tick marks along the y axis at intervals of one from negative two to two and with tick marks along the x axis at intervals of pi over three from zero to two pi. A curve drawn with a dotted line starts at the point zero comma negative two, passes through three pi over six comma zero, reaches a maximum at the point pi comma two, then changes direction to pass through the point nine pi over six comma zero followed by the point two pi comma negative two. A curve drawn with a solid line starts at the point zero comma zero, rises to the point three pi over six comma one, decreases to the point pi comma zero, increases to the point nine pi over six comma one, and decreases to the point twelve pi over six comma zero. 
  4.  A coordinate plane is shown with tick marks along the y axis at intervals of one from negative two to two and with tick marks along the x axis at intervals of pi over three from zero to two pi. A curve drawn with a dotted line starts at the point zero comma negative two, passes through three pi over six comma zero, reaches a maximum at the point pi comma two, then changes direction to pass through the point nine pi over six comma zero followed by the point two pi comma negative two. A curve drawn with a solid line passes through the point zero comma one, then decreases to the point three pi over six comma zero, then increases to the point pi comma one, then decreases to the point nine pi over six comma zero, then increases to the point twelve pi over six comma one. 

Correct Response: A. Multiplying each side of the equation in the stem by cotangent squared of x as suggested in the stem yields the equation negative 2 cosine of x equals tangent squared of x. The graph of negative 2 cosine of x will begin at negative 2 and proceed upward to reach a maximum at the point pi comma 2. The graph of tangent squared of x will begin at 0 comma 0 before increasing to infinity with an asymptote at x equals pi over 2. The graph will then decrease from infinity to the point pi comma 0 before increasing to infinity with an asymptote of x equals 9 pi over 6.

Competency 0013 
Apply the principles and techniques of integral calculus.

7. What is the solution to the equation  d y over d x equals the fraction with numerator x plus 3 and denominator y squared ?

  1.  y equals open parentheses the fraction with numerator 3 x squared and denominator 2 plus 9 x plus C close parentheses raised to the 1 third power 
  2.  y equals open parentheses x squared over 6 plus x plus C close parentheses raised to the 1 third power 
  3.  y equals open parentheses 3 x squared plus 9 x plus C close parentheses raised to the negative 1 third power 
  4.  y equals open parentheses the fraction with numerator 3 and denominator 2 x squared plus 9 x plus C close parentheses raised to the third power 

Correct Response: A. Multiplying each side of the given equation by d x yields the equation d y equals the fraction with numerator x plus 3 and denominator y squared end fraction d x. Multiplying both sides by y squared yields the equation y squared d y equals x plus three d x. Integrating each side of the equation yields y cubed over 3 plus C equals x squared over 2 plus 3 x plus C. Multiplying each side of this equation by 3 yields y cubed plus three C equals three x squared over two plus nine x plus C. Since the C on the right and the C on the left of the equation each represent different, unknown integration constants, subtracting 3 C from both sides yields y cubed equals 3 x squared over 2 plus 9 x plus C where C is an unknown integration constant. Raising each side of the equation to the 1 third power yields the correct response.

Competency 0015 
Apply the principles and properties of Euclidean geometry in two and three dimensions.

8.  start bold Use the figure below to answer the question that follows. end bold 

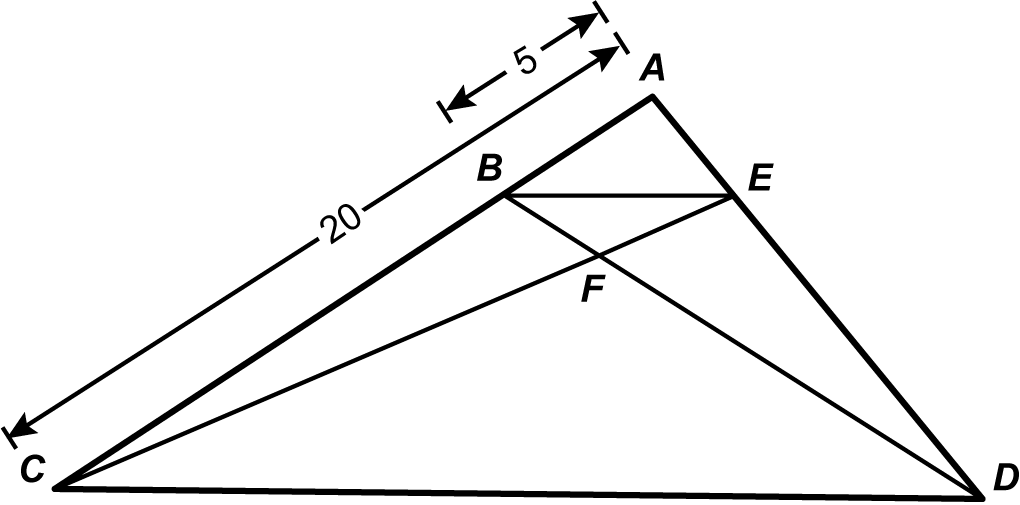
a diagram of a triangles

A triangle is drawn with vertices A, D, and C. A point, B, is located on line segment A C and a point, E, is located on line segment A D such that line segment B E is parallel to line segment C D. Line segments C E and B D are drawn, and their intersection is labeled point F.

In the figure above, the length of line segment A B is 5, the length of line segment A C is 20, and line segment B E is parallel to line segment C D. Which of the following is the ratio of the length of line segment E F to the length of line segment C E?

  1.  1 third 
  2.  1 fourth 
  3.  1 fifth 
  4.  1 sixth 

Correct Response: C. The parallel segments line segment B E and line segment C D allow the use of the alternate interior angles theorem to prove that angle B E C and angle E C D are congruent. The vertical angles theorem can be used to prove that angle B F E and angle D F C are congruent. Since two angles in triangle C F D are congruent to two angles in triangle E F B, the two triangles are similar due to the angle-angle similarity theorem. Triangle A B E and triangle A C D share angle B A E. Angle A B E and angle A C D are congruent due to the corresponding angles theorem. This means that triangle A B E and triangle A C D are also similar to one another. Since the length of line segment A B is 5 and the length of line segment A C is 20, the scale factor that maps triangle A B E onto triangle A C D is A C over A B equals 20 over 5 equals 4. As a result, since the length of line segment B E is x, the length of line segment C D must be 4 times x. Recall that triangle E F B is similar to triangle C F D. Since line segment B E corresponds to line segment C D, the scale factor that maps triangle E F B to triangle C F D is C D over B E equals 4 x over x equals 4. As a result, line segment C F is 4 times as long as line segment E F. This can be represented by the equation C F equals 4 E F, implying that C E equals C F plus E F equals 4 E F plus E F equals 5 E F. This means that the ratio of E F to C E is E F over C E equals E F over 5 E F equals 1 over 5.

Competency 0017 
Apply the principles, properties, and techniques of probability.

9.  start bold Use the work sample below to answer the question that follows. end bold 

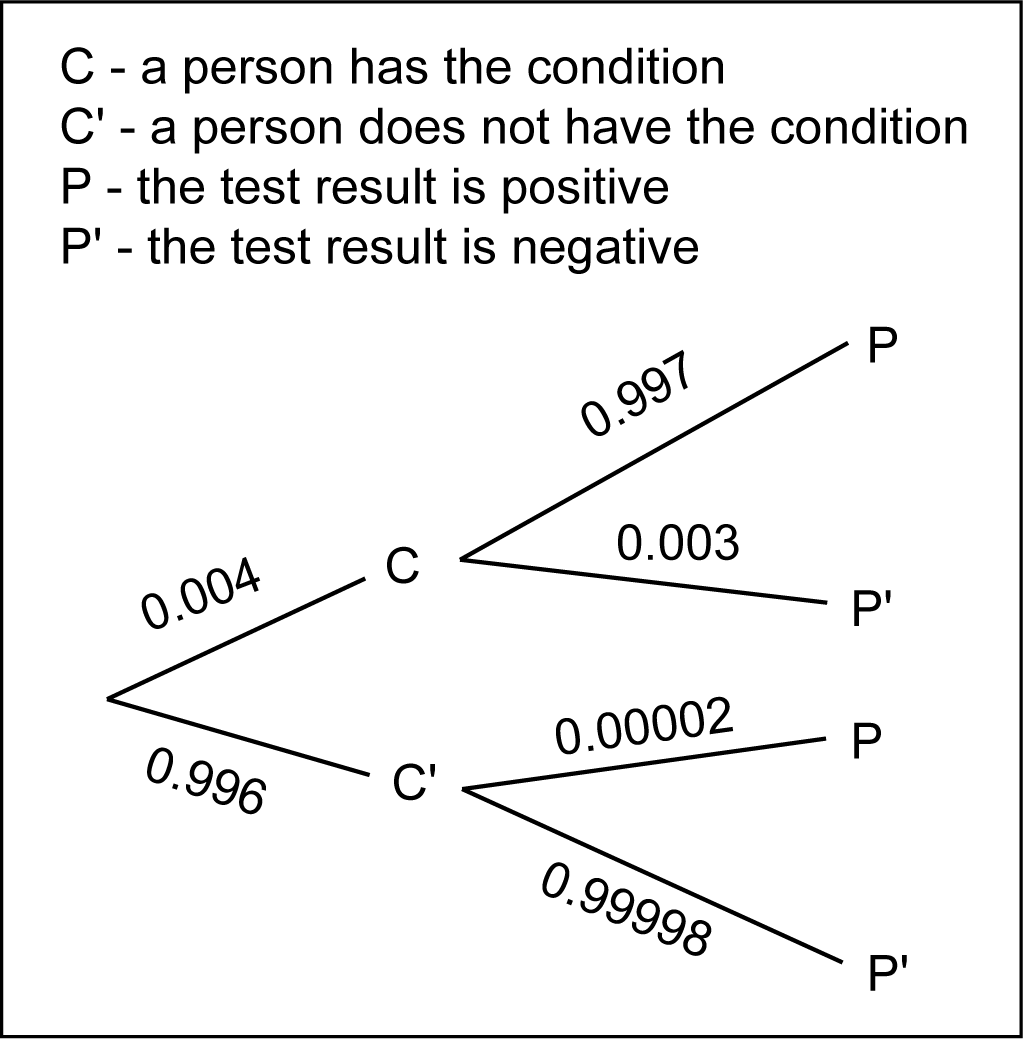
a diagram of a probability tree

A probability tree which contains information about two events. The probability of a person having a certain condition is represented by the letter C, and the probability of a person not having the condition is represented by C prime. The probability of a person’s test being positive for the condition is represented by the letter P, and the probability that the test is negative is represented by P prime. The first section of the tree has two branches. The branch labeled C has a probability of zero point zero zero four, and the branch labeled C prime has a probability of zero point nine nine six. From the end of the branch labeled C extend 2 branches labeled P and P prime. The probability on the P branch is zero point nine nine seven, and the probability on the P prime branch is zero point zero zero three. From the end of the branch labeled C prime extend two branches labeled P and P prime. The branch labeled P has a probability of zero point zero zero zero zero two. The branch labeled P prime has a probability of zero point nine nine nine nine eight.

A student constructs the tree diagram shown to model a problem about a new test that is used to detect a certain condition. Which of the following expressions can be used to find the probability that a person does not have the condition, given that the test result is negative?

  1.  the fraction with numerator 0 point 9 9 6 times 0 point 0 0 0 0 2 and denominator 0 point 0 0 4 times 0 point 0 0 3 plus 0 point 9 9 6 times 0 point 9 9 9 9 8 
  2.  the fraction with numerator 0 point 9 9 6 times 0 point 9 9 9 9 8 and denominator 0 point 0 0 4 times 0 point 0 0 3 plus 0 point 9 9 6 times 0 point 9 9 9 9 8 
  3.  the fraction with numerator 0 point 9 9 6 times 0 point 9 9 9 9 8 and denominator 0 point 0 0 4 times 0 point 9 9 7 plus 0 point 9 9 6 times 0 point 0 0 0 0 2 
  4.  the fraction with numerator 0 point 0 0 4 times 0 point 0 0 3 and denominator 0 point 0 0 4 times 0 point 9 9 7 plus 0 point 9 9 6 times 0 point 0 0 0 0 2 

Correct Response: B. Bayes’ Theorem states that for events A and B that are not independent, the probability of A given B equals the fraction with numerator the probability of B given A times the probability of A and denominator the probability of B. Therefore, the probability of C prime given P prime equals the fraction with numerator the probability of P prime given C prime times the probability of C prime and denominator the probability of P prime. The probability of a negative test given that the person does not have the condition is given in the tree as 0 point 9 9 9 9 8. Likewise, the tree indicates that the probability of not having the condition is 0 point 9 9 6. The probability of a negative test result is the sum of the probability of getting a negative test result and having the condition, and the probability of getting a negative test result and not having the condition. This can be represented as 0 point 0 0 4 times 0 point 0 0 3 plus 0 point 9 9 6 times 0 point 9 9 9 9 8 using the multiplication rule. Therefore, the probability of C prime given P prime equals the fraction with numerator the probability of P prime given C prime times the probability of C prime and denominator the probability of P prime equals the fraction with numerator 0 point 9 9 9 9 8 times 0 point 9 9 6 and denominator 0 point 0 0 4 times 0 point 0 0 3 plus 0 point 9 9 6 times 0 point 9 9 9 9 8, which is equivalent to response B.

Competency 0019 
Apply the principles of discrete mathematics.

10.  start bold Use the diagram below to answer the question that follows. end bold 

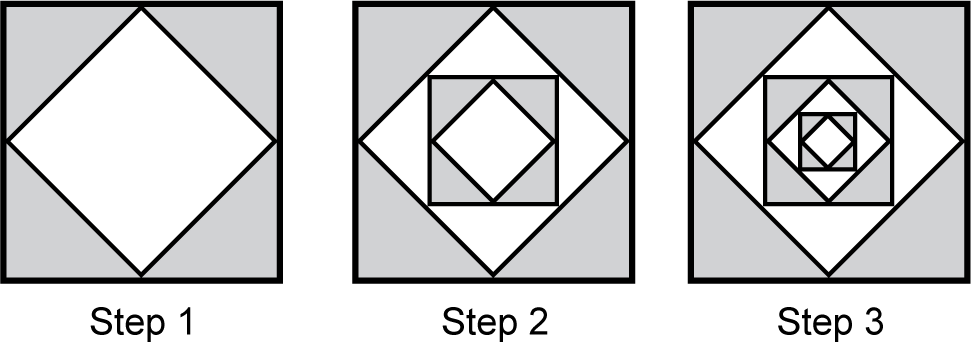
a diagram of three geometric figures

Three geometric figures are labeled step one, step two, and step three. The figure for step one consists of a large square whose midpoints are the vertices of a smaller square. The area inside the larger square but outside the smaller square is shaded. In step two, a scaled down version of the figure from step one is located in a copy of the figure from step one such that the vertices of the scaled down figure are the midpoints of the smaller inner square from step one. In step three, a further scaled down version of the figure from step one is located such that its vertices are the midpoints of the inner square of the scaled down figure from step two.

A student creates the following pattern starting with a square with an area of 1 unit squared . What fraction of the square should be shaded in Step 4?

  1.  21 over 32 
  2.  85 over 128 
  3.  171 over 256 
  4.  341 over 512 

Correct Response: B. In step 1, half of the square is shaded. In step 2, the same figure from step 1 has been scaled down and placed in the center of the figure from step 1. The scaled down portion is1 fourth the size of the original step 1 figure, and like the figure in step 1 is half-shaded. This means the shaded portion of step 2 is one half times one plus one half times one fourth. In step 3, a version of the figure in step 1 that has been scaled down by a factor of 1 sixteenth. The shaded portion of step 3 is therefore one half times one plus one half times one fourth plus one half times one sixteenth. From this, it can be determined that each step adds a version of the figure in step 1 that is one fourth to the power of the quantity n minus one in size and which is half shaded. Therefore, the shaded area in step 4 can be written as one half times one plus one half times one fourth plus one half times one sixteenth plus one half times one sixty-fourth equals 85 over 128.