Study Guide
Field 211: Advanced Mathematics
Sample Constructed-Response Assignment
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
The following materials contain:
- Test directions for the constructed-response assignment
- A sample constructed-response assignment
- An example of a strong and weak response to the assignment, and a rationale for each
- The performance characteristics and scoring scale
Test Directions for the Constructed-Response Assignment
This section of the test consists of one constructed-response assignment. You will be asked to prepare a written response of approximately 300 to 600 words on the assigned topic.
Read the assignment carefully before you begin your response. Think about how you will organize your response. You may use the erasable sheet(s) to make notes, write an outline, or otherwise prepare your response. start bold and italics However, your final response to the assignment must be either: end bold and italics
- typed into the on-screen response box,
- written on a response sheet and scanned using the scanner provided at your workstation, or
- provided using both the on-screen response box (for typed text) and a response sheet (for calculations or drawings) that you will scan using the scanner provided at your workstation.
start bold Instructions for scanning your response sheet(s) are available by clicking the "Scanning Help" button at the top of the screen. end bold
As a whole, your response must demonstrate an understanding of the knowledge and skills of the field. In your response to the assignment, you are expected to demonstrate the depth of your understanding of the content area through your ability to apply your knowledge and skills rather than by merely reciting factual information.
Your responses to the assignments will be evaluated based on the following criteria.
start bold PURPOSE: end bold the extent to which the response achieves the purpose of the assignment
start bold SUBJECT KNOWLEDGE: end bold appropriateness and accuracy in the application of subject knowledge
start bold SUPPORT: end bold quality and relevance of supporting evidence
start bold RATIONALE: end bold soundness of argument and degree of understanding of the subject areaThe constructed-response assignment is intended to assess subject matter knowledge and skills, not writing ability. However, your response must be communicated clearly enough to permit valid judgment of the scoring criteria. Your response should be written for an audience of educators in this field. The final version of your response should conform to the conventions of edited American English. Your response must be your original work, written in your own words, and not copied or paraphrased from some other work.
Be sure to write about the assigned topic. Remember to review your work and make any changes you think will improve your response.
Any time spent responding to the assignment, including scanning the response sheet(s), is part of your testing time. Monitor your time carefully. When your testing time expires, a pop-up message will appear on-screen indicating the conclusion of your test session. Only response sheets that are scanned before you end your test or before time has expired will be scored. Any response sheet that is not scanned before testing ends will start uppercase NOT end uppercase be scored.
Sample Constructed-Response Assignment
Competency 0020
Analyze a lesson plan for a given learning standard in the Oklahoma Academic Standards for Mathematics, including examples of student work and/or assessments, and describe subsequent activities that address student needs on the basis of your analysis.
start bold Use the information provided in the exhibits to complete the assignment that follows. Click on the tabs to view the information you will need. end bold
Using the data provided, prepare a response of approximately 300 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need.
start bold Class Context end bold
A Geometry class is studying the use of trigonometric ratios to solve problems involving right triangles. They have used right triangles to indirectly measure large horizontal and vertical distances in problem-solving situations. They have also practiced solving more complex problems that involve lengths and angles of multiple triangles. Additionally, the students have explored situations in which real-world factors such as the height of an observer require interpretation of a solved triangle in relevant context to determine a quantity of interest. The teacher assigns an activity to assess student ability to interpret a description of a situation involving right triangles and solve a multistep trigonometry problem. One student's work is shown in an exhibit.
start bold Excerpt from Lesson Plan end bold
start bold Course: end bold Geometry
start bold Oklahoma Academic Standards for Mathematics: end bold Geometry: Right Triangle Trigonometry ( G R T 1 point 4 )
Apply the trigonometric functions as ratios (sine, cosine, and tangent) to find side lengths in right triangles in mathematical models, including the coordinate plane.
start bold Lesson Objective: end bold Students will solve real-world problems using trigonometric ratios that involve multiple right triangles.
start bold Previous Knowledge Needed: end bold Systems of linear equations; modeling with algebraic expressions; writing and solving trigonometric equations for right triangles.
start bold Student Work end bold
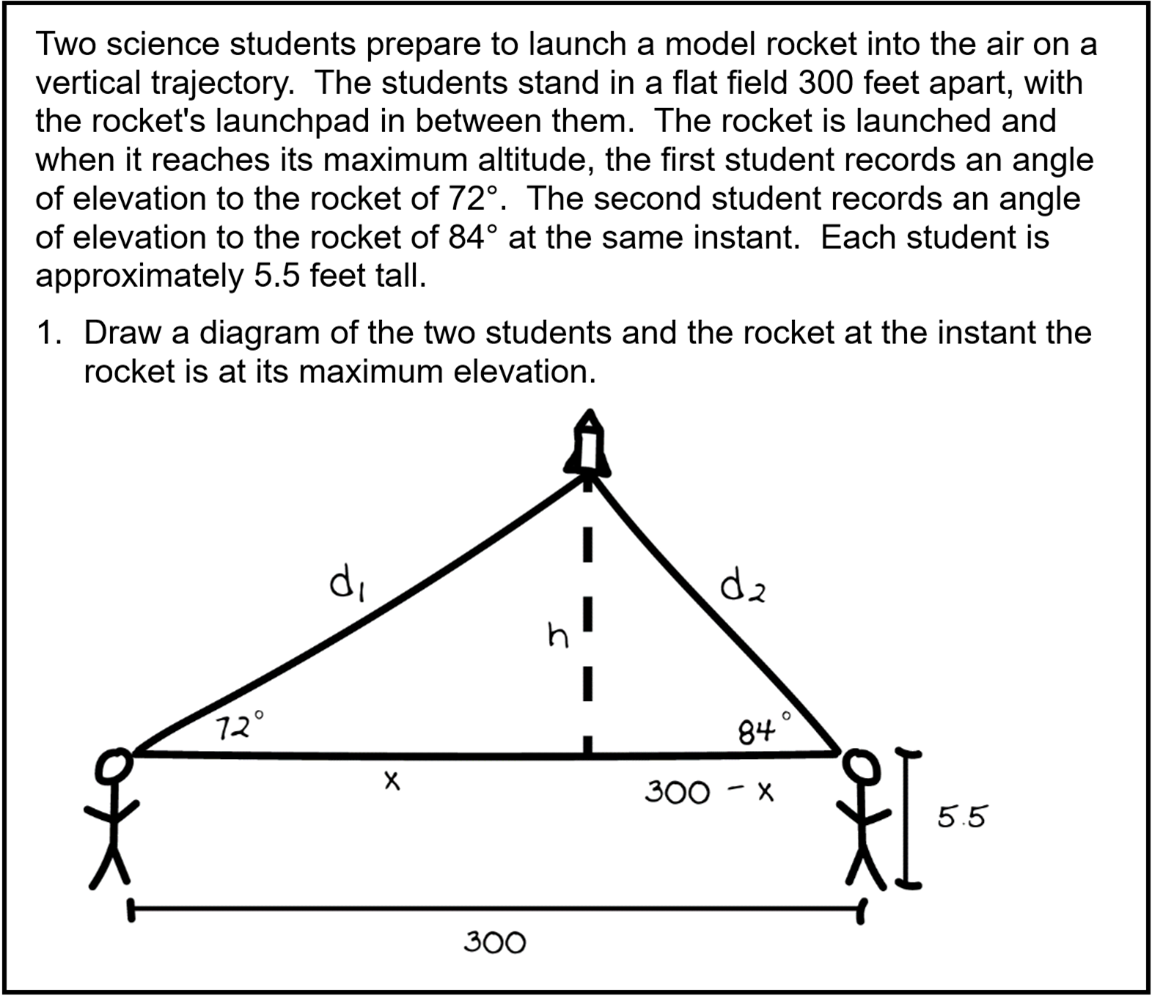
A student drawn image of two people standing three hundred units apart staring at a rocket that is in the air between them. Each person is labeled five point five units tall. A triangle is formed with vertices at the top of each personís head and a vertex at the rocket. There is an altitude drawn from the vertex at the rocket to the opposite side of the triangle, labeled h. This altitude divides the bottom side of the triangle into two segments, with the left segment labeled x and the right segment labeled three hundred minus x. The interior angle on the left of the triangle has a measure of seventy two degrees, and the interior angle on the right of the triangle has a measure of eighty four degrees. The side of the triangle that extends from the person on the left to the rocket is labeled d one, and the side of the triangle that connects the rocket to the person on the right is labeled d two.
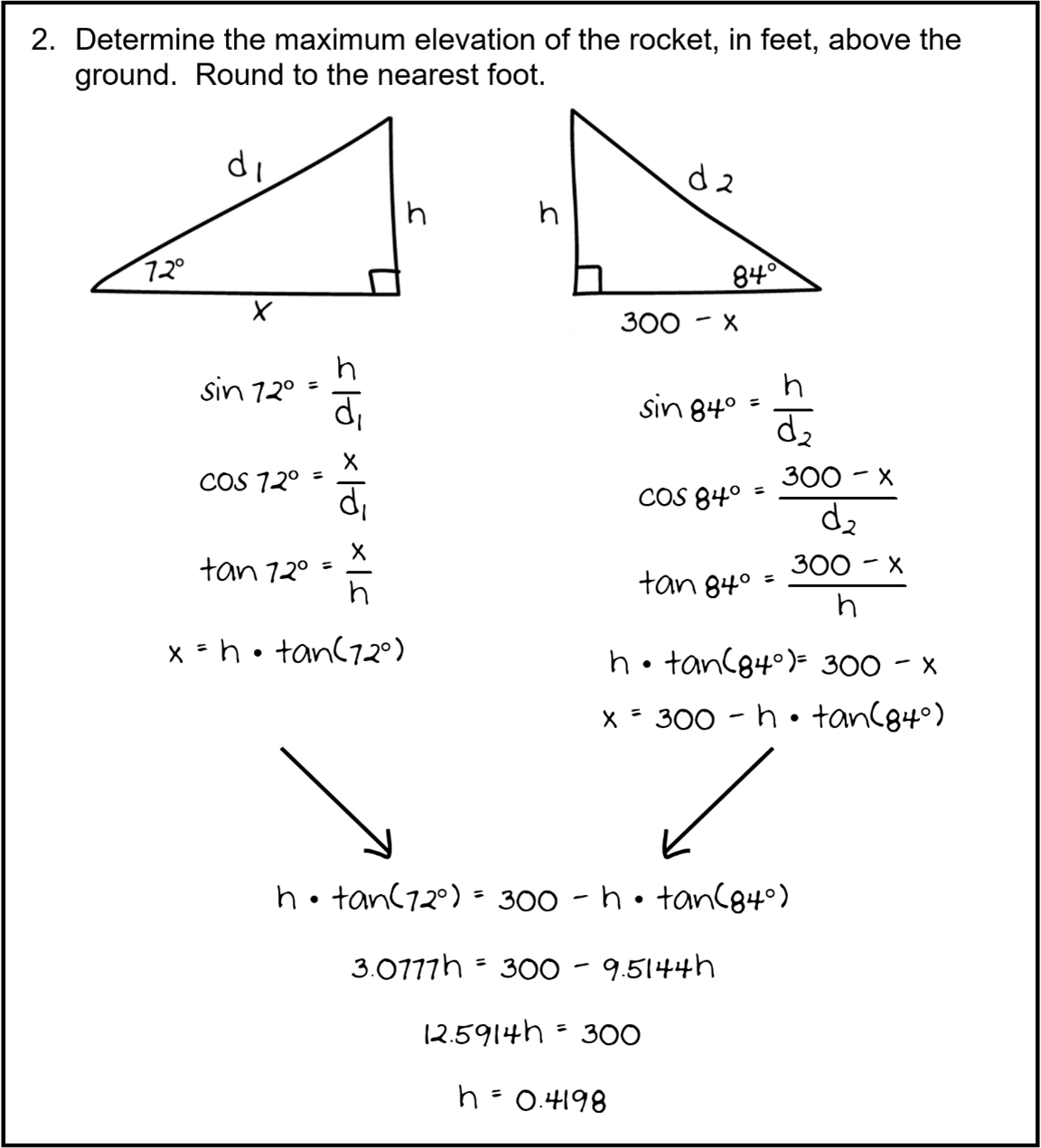
A student drawn image with two right triangles. The right triangle on the left has legs x and h, and hypotenuse d one. The included angle between d one and x is seventy two degrees. Beneath the triangle is a series of equations: Sine of seventy two degrees equals h divided by d one, cosine of seventy two degrees equals x divided by d one, and tangent of seventy two degrees equals x divided by h. The last equation reads x equals h times tangent of seventy two degrees.
The right triangle on the right has legs labeled h and three hundred minus x, with hypotenuse d two. The included angle between three hundred minus x and d two is eighty four degrees. Beneath the triangle is a series of equations: sine of eighty four degrees equals h divided by d two, cosine of eighty four degrees equals three hundred minus x divided by d two, and tangent of eighty four degrees equals three hundred minus x divided by h. Two additional equations are written below the three mentioned above: the first reads h times tangent of eighty four degrees equals three hundred minus x. The last equation reads x equals three hundred minus h times tangent of eighty four degrees.
Arrows connect the final equations on the right and left to another series of equations: h times tangent of seventy two degrees equals three hundred minus h times tangent of eighty four degrees, then three point zero seven seven seven h equals three hundred minus nine point five one four four h, then twelve point five nine one four h equals three hundred, then h equals zero point four one nine eight.
Sample Strong Response to the Constructed-Response Assignment
start bold Please note: The sample response provided below is for review purposes only and should not be used in a response on an operational exam. Use of the exact words and phrases presented in this sample response will result in a score of "U" (Unscorable) due to lack of original work. end bold
The given Geometry class is studying trigonometric ratios to learn how to solve problems involving right triangles. Students in the class will apply the trigonometric functions as ratios to find side lengths in right triangles and in real-world mathematical problems (class context).
The student work sample demonstrates several strengths related to Oklahoma Academic Standards for Mathematics G R T 1 point 4 . First, the student work sample shows the student can interpret the written description of a complex situation and synthesize that information into a diagram. Additionally, the student was able to identify sine and cosine correctly and provide the ratios in the problem. The student indicated that sine of 72 degrees was H over D 1 and sine of 84 would be H over D 2 (student work sample). The student was also able to correctly identify opposite and adjacent sides as well as the hypotenuse of the angle as shown in the work sample. Lastly, the student recognized the common leg of the multiple right triangles as per the stated standards. Even with the error, the student correctly processed the algebraic equation to determine an answer for the height.
The student did make a few errors which led to an overall incorrect answer. The major error the student made was that they reversed the ratio for tangent. The student defined the tangent ratio as the adjacent side to the reference angle divided by the opposite side to the reference angle (adjacent/opposite). The correct tangent ratio is the reciprocal of the ratio the student wrote (opposite/adjacent). The correct ratio for tangent is opposite/adjacent. The student identified tangent as adjacent/opposite for both triangles. This error in part led to the incorrect height calculated in the student work sample. The student also did not consider the height of their eyes above the ground and should have added 5 point 5 feet (66 inches) to their final height, although the calculation would still have been wrong. These errors in the student work resulted in the student obtaining a much smaller altitude than was correct.
I would use the studentís strengths of synthesizing complex scenarios and translating them into diagrams along with their correct understanding of sine and cosine to help the student better understand and use the tangent ratio. I would work one-on-one with the student, use questioning, and provide additional practice to help the student improve on this given area of need.
First, I would have the student calculate the height of a structure with a known height (i.e., a basketball hoop) that can be found on the school grounds. The student should be able to discover they are short by the stated 5 point 5 feet. I would ask them why this was short and continue to question them until they determined the source of the error.
To address the incorrect determination of the tangent ratio, I would provide additional practice and questioning to help the student. First, I would ask how the student came up with the ratio and if it was a one-time error or if it was a misconception about the tangent ratio. To address a misconception about tangent, I would give the student additional practice. We would start with a Pythagorean triangle (a right triangle with side lengths 3, 4, and 5) and have the student calculate the angle using the tangent of one of the angles (first, letting the student calculate this on their own, using the studentís incorrect ratio). Then I would have the student look up the angles and realize they did not come up with the correct angle measurement and why. It would be the inverse of the angle. I would then have the student calculate the angle again using the correct ratio. I would provide additional practice materials until the student was able to recognize tangent is opposite over adjacent.
Rationale for the Sample Strong Response
start bold Please note that the response is evaluated based upon the four performance characteristics of Purpose, Subject Matter Knowledge, Support, and Rationale. Please also note how the score point descriptions are based upon how the examinee attends to the performance characteristics. You should be very familiar with the CEOE performance characteristics and score scale and refer to them when reviewing this rationale. end bold
The response generally fulfills the purpose of the assignment (refer to the instructions for the assignment) by adequately responding to all elements of the prompt. The response addresses all parts of each bullet point of the prompt. For example, the response identifies a significant mathematical strength related to the given standard by explaining the student work sample shows an understanding of how to determine sine and cosine, and the response cites evidence from the exhibits (i.e., "The student indicated that sine of 72 degrees was H over D 1 and sine of 84 would be H over D 2 "). The response addresses the second bullet point by explaining an area of need from the student work sample Ė explaining that the student work sample showed the student defined the tangent ratio incorrectly (i.e., "The student defined the tangent ratio as the adjacent side to the reference angle divided by the opposite side to the reference angle (adjacent/opposite)"). The response addresses the last bullet by providing a student-centered instructional intervention that should help the given student learn the correct tangent ratio.
The response demonstrates a largely accurate understanding of subject matter knowledge by correctly identifying a strength related to the prompt. The identified strength is related to the state standards as required. The response identified a weakness. Although one is not directly related to geometry, the height error relates to the real-world problems part of the standard. Additionally, recognizing the error in setting up the tangent calculation does relate directly to geometry.
The supporting evidence generally supports the discussion. There are some specific examples given and elaborated upon. The examples are appropriate to the content and level of specificity needed to show the candidate does understand the material. The intervention is student-focused and does not just reteach or repeat the lesson. Lastly, the response reflects a general understanding of the topic as the response is clear, reasoned, and appropriate for the target audience. The strengths and weaknesses are based on the standards and related to the topic. The intervention is doable and would lead the student to discover their errors and how to correct them. The intervention utilizes their strengths and builds upon them. Overall, the purpose of this response is largely achieved.
Sample Weak Response to the Constructed-Response Assignment
start bold Please note: The sample response provided below is for review purposes only and should not be used in a response on an operational exam. Use of the exact words and phrases presented in this sample response will result in a score of "U" (Unscorable) due to lack of original work. end bold
The Lesson Objective for this class is for students to solve real-world problems using trigonometric ratios that involve multiple right triangles. The students in the class have previously been learning about systems of linear equations and also modeling with algebraic expressions. Given this background, students in the class are given a word problem to solve. The word problem asks students to draw a diagram and then calculate maximum elevation.
The student work sample shows what one student in the class did to complete this assignment. The student did a good job overall. The student work sample is well written and laid out in an organized manner. The student was able to diagram the scenario adequately and demonstrate the ability to cross multiply in order to solve the equation. The student recognized that if two statements are each equal to the same solution, the statements must be equal to each other. I believe this is called the transitory property in algebra.
The student work sample also shows that the student has an error in their work. The error is that the student has the incorrect height. The student did the math correctly but set up the equation for tangent wrong. The factors are inverted in the student work sample.
There are many interventions that the teacher can do here to correct the studentís error. In order to correct the studentís misunderstanding, the teacher should give the student a worksheet of similar word problems and after reviewing how to calculate the lengths of sides using tangent, have the student complete the worksheet. The teacher can then have the student look at an answer sheet to see what they got right or wrong.
Rationale for the Sample Weak Response
start bold Please note that the response is evaluated based upon the four performance characteristics of Purpose, Subject Matter Knowledge, Support, and Rationale. Please also note how the score point descriptions are based upon how the examinee attends to the performance characteristics. You should be very familiar with the CEOE performance characteristics and score scale and refer to them when reviewing this rationale. end bold
The purpose of this assignment is partially achieved. While the response does address all parts of the prompt, it does so in a very superficial and limited way.
The application of subject matter knowledge is limited or weak throughout the response. Though the response does identify a strength and a weakness and propose an intervention, it does not fully demonstrate the candidate has subject matter knowledge. It provides examples from the student work sample; however, the examples are weak and lack specificity (i.e., while diagramming the situation is valuable, it does not strongly tie to the standards). Diagramming the scenario is connected to the goal of a real-world problem; however, it is limited in its applicability. Additionally, algebraic manipulation is a previous skill, not part of the stated learning goal for this lesson. The weakness is related to the goal; however, the term inverted is unclear, and the response does not demonstrate what they mean (for instance, the response could have discussed adjacent/opposite versus opposite/adjacent).
The supporting evidence is limited with few relevant examples throughout the response. The response does provide a strength and two weaknesses. Unfortunately, it does not cite evidence from the sample work. The response mentions the height is wrong but does not say why. Additionally, the response says that tangent was set up wrong but again does not say why or give the correct ratio. A strong response would expand on both of those errors.
Lastly, the rationale is limited. The intervention is not student-focused and does not build on the student strengths. While the strengths and weaknesses are correct, they are lower-level examples and do not demonstrate the candidate fully understands the scenario. Overall, the response demonstrates a limited, poorly reasoned understanding of the topic.
Performance Characteristics
The following characteristics guide the scoring of responses to the constructed-response assignment.
Scoring Scale
Scores will be assigned to each response to the constructed-response assignment according to the following scoring scale.
