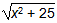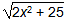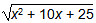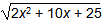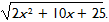Study Guide
Field 111: Advanced Mathematics
Sample Selected-Response Questions
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
General Test Directions
This test contains two sections: (1) a section with selected-response questions and (2) a constructed-response section. The directions for the constructed-response assignment appear before that section.
Each question in the first section is a selected-response question with four answer choices. Read each question and answer choice carefully and choose the start uppercase ONE end uppercase best answer. Try to answer all questions. In general, if you have some knowledge about a question, it is better to try to answer it. You will start uppercase NOT end uppercase be penalized for guessing.
A calculator is available to you for this test. To access the calculator, click on the
icon located in the upper left corner of the screen. A pop-up window containing the calculator will appear. You can reposition the calculator by placing your cursor in the blue area above the calculator and dragging the window to the location of your choice.
Use the numbers on the keyboard and/or point and click with the mouse to enter your computations into the on-screen calculator. When you are finished, close the calculator by clicking the
button in the upper right corner of the calculator.
Reference materials will also be available to you during this test. To access these reference materials, click on the
icon located in the lower left corner of the screen.
You may work on and complete the selected-response questions and the constructed-response assignment in any order that you choose. Be sure to allocate your time carefully so that you are able to complete the entire test within the testing session.
Use of any other type of calculator or outside reference materials during the testing session is prohibited.
Sample Selected-Response Questions
Competency 0002
Apply knowledge of number theory and the complex number system.
1. start bold Use the diagram below to answer the question that follows. end bold
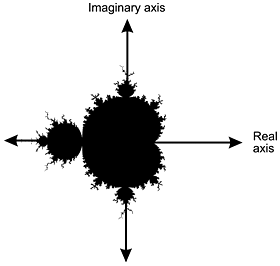
The diagram shows a graph in which the horizontal axis is labeled Real axis and the vertical axis is labeled Imaginary axis. The shape plotted resembles an ovoid centered around the origin, dented in at the Real axis on the right, with a large circular appendage on the left and two smaller ones at the top and bottom. Most of the perimeter sprouts rootlike bulbs and tendrils.
Given that a complex number z equals a plus b i is an element of the set represented by the shaded region of the complex plane in the diagram, which of the following must also be an element of the set?
- A minus B I
- negative B plus A I
- 1 over the quantity A plus B I
- left paren A plus B I right paren squared
Correct Response: A. A complex number z equals a plus b i can be represented in the complex plane as an ordered pair left paren a comma b right paren, where a is the real part and b is the imaginary part of the complex number z. Since the set in the diagram is symmetric about the x-axis, if left paren a comma b right paren is an element of the set, then its reflection about the x-axis left paren a comma negative b right paren, or a minus b i, will also be an element of the set.
Competency 0005
Analyze the principles and properties of linear algebra.
2. start bold Use the problem below to answer the question that follows. end bold
A stable contains only people and horses. If there are 94 legs and 27 heads in the stable, how many people and how many horses does it contain?
The problem can be solved using which of the following matrix equations?
Each response is a matrix equation in which a 2 by 2 matrix is multiplied by a 2 by 1 matrix to yield a 2 by 1 matrix.
-
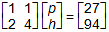 Response A. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, p, second row, h. Equals third matrix, first
row 27, second row, 94.
Response A. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, p, second row, h. Equals third matrix, first
row 27, second row, 94. -
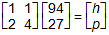 Response B. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, 94, second row, 27. Equals third matrix,
first row h, second row, p.
Response B. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, 94, second row, 27. Equals third matrix,
first row h, second row, p. -
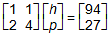 Response C. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, h, second row, p. Equals third matrix, first
row 94, second row, 27.
Response C. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, h, second row, p. Equals third matrix, first
row 94, second row, 27. -
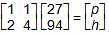 Response D. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, 27, second row, 94. Equals third matrix,
first row, p, second row, h.
Response D. First matrix, first row, 1, 1, second row, 2, 4.
Multiplied by second matrix, first row, 27, second row, 94. Equals third matrix,
first row, p, second row, h.
Correct Response: A. Let p equals the number of people and h equals the number of horses in the stable. Since people and horses each have one head, 1 p plus 1 h equals 27. Likewise, since people have two legs and horses have four, 2 p plus 4 h equals 94. This system of equations is equivalent to the matrix equation in response A, which can be verified by performing the given matrix multiplication.
Competency 0007
Analyze the properties of quadratic and higher-order polynomial relations and functions.
3. start bold Use the graph below to answer the question that follows. end bold
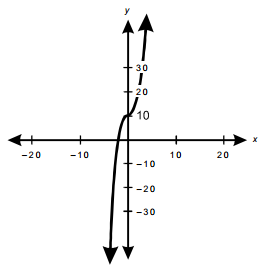
The graph is an x, y plot. The x axis is labeled from negative 20 to 20 in increments of 10, and the y axis is labeled from negative 30 to 30 in increments of 10. The data line ascends through the lower left quadrant close to the y axis, crosses the x axis at about negative 2, curves almost horizontally through the y axis at 10, then curves upward and continues out of the upper right quadrant close to the y axis.
The function f left paren x right paren equals 2 x cubed plus 10 is graphed above. Which of the following functions represents a translation of f left paren x right paren three units in the positive x-direction?
- g left paren x right paren equals 2 x cubed plus 13
- g left paren x right paren equals 6 x cubed plus 30
- g left paren x right paren equals 2 x cubed minus 18 x squared plus 54 x minus 44
- g left paren x right paren equals 2 x cubed plus 18 x squared plus 54 x plus 64
Correct Response: C. Given a function f left paren x right paren, f left paren x minus a right paren represents a translation by A units in the positive X-direction. Therefore, given f left paren X right paren equals 2 x cubed plus 10 and a equals 3, f left paren x minus 3 right paren equals g left paren x right paren equals 2 left paren x minus 3 right paren cubed plus 10 represents a translation by three units in the positive X-direction. Cubing the binomial and simplifying gives g left paren x right paren equals 2 x cubed minus 18 x squared plus 54 x minus 44.
Competency 0009
Apply the principles and properties of exponential and logarithmic functions.
4. At the time that it stopped advertising, a manufacturing company had sales of 80,000 units per month. Four months later, its sales had dropped to 60,000 units per month. The company's sales can be expressed by the function y equals C e to the k t, where t represents the number of months since the company stopped advertising and y represents the number of units sold per month. What will the predicted sales be six months after the company stopped advertising?
- 49,746 units per month
- 50,000 units per month
- 51,968 units per month
- 52,500 units per month
Correct Response: C. Using y equals C e to the k t when t equals 0, 80,000 equals C e to the 0, so C equals 80,000. When t equals 4, 60,000 equals 80,000 times e to the 4 k and e to the 4 k equals 3 fourths. Taking the natural log of both sides and solving for K, k equals the natural log of 3 fourths over 4 equals approximately negative 0.0719. The predicted sales after six months will be y equals 80,000 e to the negative 0.0719 times 6 equals approximately 51,968 units per month.
Competency 0013
Apply the principles and techniques of differential calculus.
5. start bold Use the graph below to answer the question that follows. end bold
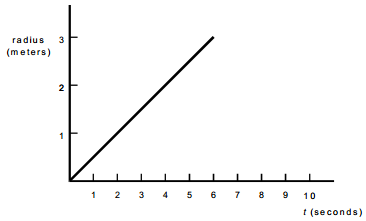
The graph's horizontal axis is labeled t in seconds, with values labeled from 0 to 10 in increments of 1. The vertical axis is labeled radius in meters, with values labeled from 0 to 3 in increments of 1. The data plot is a straight line from the origin to 3 meters at 6 seconds.
The graph shows the radius of a spherical balloon as a function of time. What is the approximate rate of change in cubic meters per second of the volume of the balloon at t equals 4 s
- 2.67 pi
- 8 pi
- 32 pi
- 64 pi
Correct Response: B. The volume of a sphere (from the formulas pages) is V equals 4 thirds pi r cubed. To determine the rate of change of the volume as a function of time, differentiate the expression implicitly to obtain dV over dt equals 4 pi r squared d r over d t, since the radius r of t is a function of time. From the graph, the value of r at t equals 4 seconds is 2 meters. The derivative of r of t, d r over d t, at t equals 4 seconds is the slope of the line tangent to the curve at t equals 4, which is 1 half. Substituting these values into the expression results in d V over d t equals 4 pi 2 squared times 1 half equals 8 pi.
Competency 0014
Apply the principles and techniques of integral calculus.
6. start bold Use the problem below to answer the question that follows. end bold
Find the volume of the solid of revolution formed by rotating about the x-axis the region bounded by y equals 2 x y equals 0 x equals 3 and x equals 5
Which of the following definite integrals could be evaluated to solve the problem?
Correct Response: B. The volume can be calculated by dividing the solid into a series of cylindrical disks, each having radius r equals f of x and height h equals delta x. Therefore, the volume V equals the limit as delta x approaches 0 of the sum pi r squared h equals the integral from a to b pi times the square of f of x, dx. Given that f of x equals 2 x, a equals 3, b equals 5, V equals the integral from 3 to 5 pi the square of 2x, dx
Competency 0016
Apply the principles and properties of Euclidean geometry in two and three dimensions.
7. In a right triangle, the length of one leg is x and the length of the second leg is 5 units longer. What is the length of the hypotenuse?
Correct Response: D. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. Thus, h squared equals x squared plus the square of the sum of x plus 5 and h squared equals x squared plus x squared plus 10 x plus 25 and finally, h equals the square root of the quantity 2x squared plus 10 x plus 25.
Competency 0017
Apply the principles and properties of coordinate geometry.
8. start bold Use the diagram below to answer the question that follows. end bold
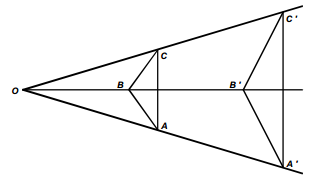
The diagram shows a triangle, A B C. Its longest side, A C, is vertical, with vertex B to the left of side A C. The other two sides appear to be equal in length. To the right of triangle A B C is a second, triangle, A prime, B prime, C prime, which is a transformation of triangle ABC. It is larger than triangle ABC. Side A prime B prime is vertical, with vertex B prime to the left of side A prime C prime. A horizontal line passes through vertex B and vertex B prime. Another line passes through vertex C and vertex C prime, and a third line passes through vertex A and vertex A prime. The three lines that pass through the vertices of both triangles converge at point O, to the left of both triangles.
The transformation T of Triangle A B C to triangle A prime B prime C prime is a dilation with center at O. If the area of triangle A prime B prime C prime is twice the area of triangle A B C, what is the scale factor of T?
- 1 half
- the square root of 2
- 2
- 4
Correct Response: B. A dilation is a similarity transformation. Therefore, triangle ABC is similar to triangle A prime B prime C prime. If the dilation has scale factor k, then the length of each linear dimension is multiplied by k, and the area left paren length times length right paren will be multiplied by k squared. Therefore, the area of triangle A prime B prime C prime equals k squared times the area of triangle ABC equals 2 times the area of triangle ABC. Therefore, k squared equals 2 and k equals the square root of 2.
Competency 0018
Apply the principles, properties, and techniques of probability.
9. start bold Use the diagram below to answer the question that follows. end bold
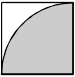
A target consists of a square region in which a quarter circle is drawn and shaded. The radius of the circle is equal to one side of the square. A computer program calculates pi by simulating darts being fired randomly at the target. A success is defined as a dart falling within the shaded area. If the computer obtains a value of 3.12 after 1000 shots at the target, how many darts landed in the shaded area? (Assume the probability of hitting the target is 1.)
- 312
- 624
- 750
- 780
Correct Response:D. Let N represent the number of darts that land in the shaded area. The probability that N darts land in the quarter circle is equal to the ratio of the area of the quarter circle to the area of the square. Let S represent the length of the side of the square. Since the area of a circle is pi s squared, N over 1000 equals pi over 4 times s squared all over s squared, Substituting 3.12 for the value obtained for pi by the computer and simplifying and solving the equation for N results in N equals 780
Competency 0019
Apply the principles, properties, and techniques of statistics.
10. When a computer manufacturing company receives a shipment of computer chips, its quality control inspectors randomly select 10 percent of the chips in the shipment on which to run tests. If 10 percent or more of the chips in the sample are defective, the entire shipment is rejected. Which of the following assumptions underlies this decision to test only a sample of chips rather than the entire shipment?
- If there are any defects in the shipment, they are most likely to appear in the 10 percent selected for testing.
- The chances of having to reject the load increase as the number of chips increases.
- The small sample is fairly representative of the overall shipment.
- The probability for human error in the testing procedures increases as the sample size increases.
Correct Response: C. The central limit theorem allows inferences about a population (in this case the shipment of computer chips) to be made from a random sample chosen from the population. These inferences are generally stated in terms of probabilities. In the case given, the quality control engineers are assuming that there is a high probability that the sample represents the population, which is equivalent to response C.

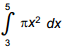
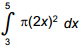
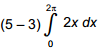
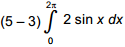
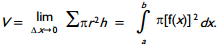
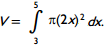 .
.