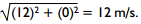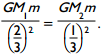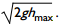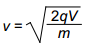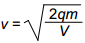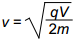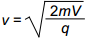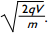Study Guide

Field 014: Physics 
Sample Selected-Response Questions

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

Expand All | Collapse All

General Test Directions

This test contains two sections: (1) a section with selected-response questions and (2) a constructed-response section. The directions for the constructed-response assignment appear before that section.

Each question in the first section is a selected-response question with four answer choices. Read each question and answer choice carefully and choose the  start uppercase ONE end uppercase  best answer. Try to answer all questions. In general, if you have some knowledge about a question, it is better to try to answer it. You will  start uppercase NOT end uppercase  be penalized for guessing.

A calculator is available to you for this test. To access the calculator, click on the icon located in the upper left corner of the screen. A pop-up window containing the calculator will appear. You can reposition the calculator by placing your cursor in the blue area above the calculator and dragging the window to the location of your choice.

Use the numbers on the keyboard and/or point and click with the mouse to enter your computations into the on-screen calculator. When you are finished, close the calculator by clicking the button in the upper right corner of the calculator.

Reference materials will also be available to you during this test. To access these reference materials, click on the icon located in the lower left corner of the screen.

You may work on and complete the selected-response questions and the constructed-response assignment in any order that you choose. Be sure to allocate your time carefully so that you are able to complete the entire test within the testing session.

Use of any other type of calculator or outside reference materials during the testing session is prohibited.

Sample Selected-Response Questions

Competency 0001 
Apply knowledge of scientific inquiry and experimental and engineering design.

1.  start bold Use the diagram below to answer the question that follows. end bold 

   

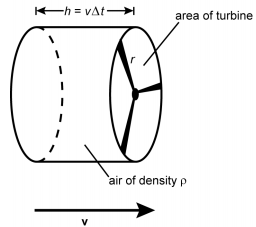
The diagram shows the three blades of a wind turbine. A circle describes the sweep of the tips, and the resulting disk is labeled area of turbine. The radius is marked r. A cylinder is drawn, with the disk of the turbine forming one end of the cylinder. The cylinder is labeled air of density rho, and the length of the cylinder is dimensioned as h equals v increment t.

Students are developing a model of a wind turbine. To estimate the maximum theoretical power the turbine can generate, they assume that all of the energy in a column of air of density ρ  rho  traveling at speed v having the dimensions shown is converted to electrical energy. If the radius of the blades of the turbine is r, which of the following expressions gives the maximum power obtainable?

1. ¹/₂ρv²  1 half rho V squared 
2. ^ρv2/_2Δt  rho v squared over 2 increment t 
3. ¹/₂ρπr²v³ 1 half rho pi r squared v cubed
4. ¹/₂ρv²  1 half rho v squared 

Answer

Correct Response: D.

The volume of air passing through the wind turbine in a time interval Δt  increment t  represents a cylinder of length vΔt  v increment t  and with a base area of πr².  pi r squared  The volume of air is thus vΔtπr².  v increment t pi r squared  Multiplying this volume by the air density ρ rho  gives the mass of the air, m. The kinetic energy of this air mass is KE = ¹/₂mv²  K E equals 1 half m v squared  which is equal to KE = ¹/₂ρΔtπr²v³.  K E equals 1 half rho increment t pi r squared v cubed  Since power is the rate of change of energy with respect to time, the maximum power obtainable is the rate at which this kinetic energy can be converted to electric energy, which is found by dividing the kinetic energy by Δt,  increment t  to result in ¹/₂ρπr²v³.  1 half rho pi r squared v cubed. 

Correct Response: D. The volume of air passing through the wind turbine in a time interval increment t represents a cylinder of length v increment t and with a base area of pi r squared The volume of air is thus v increment t pi r squared Multiplying this volume by the air density rho gives the mass of the air, m. The kinetic energy of this air mass is K E equals 1 half m v squared which is equal to K E equals 1 half rho increment t pi r squared v cubed Since power is the rate of change of energy with respect to time, the maximum power obtainable is the rate at which this kinetic energy can be converted to electric energy, which is found by dividing the kinetic energy by increment t, to result in 1 half rho pi r squared v cubed

---

Competency 0003 
Analyze motion in one and two dimensions.

2. A mass is projected from ground level at an angle of 60°  60 degrees  with respect to the horizontal with a speed of 24 m/s. 24 meters per second. What is the speed of the mass at its maximum height?

1. 0.0 m/s  0.0 meters per second 
2. 4.0 m/s  4.0 meters per second 
3. 12 m/s  12 meters per second 
4. 21 m/s  21 meters per second 

Answer

Correct Response: C.

The projected mass follows a two-dimensional trajectory that has horizontal and vertical velocity components. The horizontal velocity component remains constant throughout the trajectory because there are no net horizontal forces acting on the mass. From triangle trigonometry, the horizontal component is given by 24cos60° m/s,  24 cosine 60 degrees meters per second  which is equal to 12 m/s.  12 meters per second  Since the vertical velocity component is zero at the maximum height, the velocity of mass at this point is equal to the horizontal velocity component, 12 m/s.  12 meters per second  The speed is the magnitude of the velocity which equals

Correct Response: C. The projected mass follows a two-dimensional trajectory that has horizontal and vertical velocity components. The horizontal velocity component remains constant throughout the trajectory because there are no net horizontal forces acting on the mass. From triangle trigonometry, the horizontal component is given by 24 cosine 60 degrees meters per second, which is equal to 12 meters per second. Since the vertical velocity component is zero at the maximum height, the velocity of mass at this point is equal to the horizontal velocity component, 12 meters per second. The speed is the magnitude of the velocity which equals the square root of 12 squared plus 0 squared equals 12 meters per second.

---

Competency 0005 
Apply the laws of motion to systems of particles and simple harmonic motion.

3.  start bold Use the diagram below to answer the question that follows. end bold 

  

The diagram is a horizontal line with a point labeled M sub 1 at the left end and a point labeled M sub 2 at the right end. A point labeled P is on the line between them. The distance from point M sub 1 to point P is dimensioned as 2 thirds, and the distance from point P to point M sub 2 is dimensioned as 1 third.

The diagram above shows two point masses, M₁  M sub 1  and M₂,  M sub 2  separated by a distance of 1 unit. If the net gravitational force on a third point mass at P is zero, which of the following equations represents the value of M₂  M sub 2 ?

1. M₂ = ¹/₉M₁  M sub 2 equals 1 ninth M sub 1. 
2. M₂ = ¹/₄M₁  M sub 2 equals 1 fourth M sub 1. 
3. M₂ = ¹/₃M₁  M sub 2 equals 1 third M sub 1. 
4. M₂ = ¹/₂M₁  M sub 2 equals 1 half M sub 1. 

Answer

Correct Response: B.

The gravitational force at any point along the line joining the two masses has a horizontal component only. If a point mass m is located at P the force from M₁  M sub 1  points to the left, and the force from M₂  M sub 2  points to the right. For the net gravitational force to be zero at point P, the magnitude of the force from each mass must be equal. The magnitude of the gravitational field of a point mass M on mass m is ^GMm/_{r ²}.  G M m over r squared.  Therefore, at point P  Solving this equation for M₂  M sub 2  results in M₂ = ¹/₄M₁.  M sub 2 equals 1 fourth M sub 1. 

Correct Response: B. The gravitational force at any point along the line joining the two masses has a horizontal component only. If a point mass m is located at P the force from M sub 1 points to the left, and the force from M sub 2 points to the right. For the net gravitational force to be zero at point P, the magnitude of the force from each mass must be equal. The magnitude of the gravitational field of a point mass M on mass m is G M m over r squared. Therefore, at point P times G M sub 1 m over 2 thirds squared equals G M sub 2 m over 1 third squared. Solving this equation for M sub 2 results in M sub 2 equals 1 fourth M sub 1.

---

Competency 0006 
Apply the principles of the conservation of energy and momentum.

4.  start bold Use the diagram below to answer the question that follows. end bold 

   

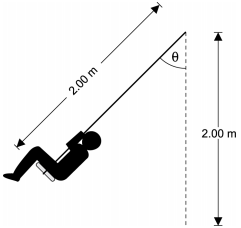
The diagram shows a child on a swing, with the swing partway up the forward part of its arc of motion. The length of the rope and the vertical dimension of its arc are dimensioned as 2.00 meters. The angle between the current position of the rope and the vertical is dimensioned as theta.

The length of each of the swing ropes on the playground swing shown above is 2.00 meters. What is the maximum speed attainable on the swing if the maximum value of θ is 45.0°?  theta is 45.0 degrees? 

1. 1.40 m/s  1.40 meters per second 
2. 2.00 m/s  2.00 meters per second 
3. 3.39 m/s  3.39 meters per second 
4. 8.85 m/s  8.85 meters per second 

Answer

Correct Response: C.

Define the potential energy at the lowest point of the path of the swing to be zero. At this point the swing attains its maximum speed and its total mechanical energy is kinetic energy only. When the swing is at its maximum height, h_max  h sub max  (θ = 45°),  left paren theta equals 45 degrees right paren,  the total energy is potential energy only. By the principle of the conservation of mechanical energy, mgh_max = ¹/₂mv²_max, or v_{max =} M G H sub max equals 1 half m v squared sub max or V sub max equals the square root of 2 G H sub max Using triangle trigonometry, h_max = 2 m − 2cos45° m = .586 m. h sub max equals 2 m minus 2 cosine 45 degrees m equals .586 meters Using g = 9.8 m/s², g equals 9.8 meters per second squared and substituting these values into the expression above, results in v_max = 3.39 m/s.  v sub max equals 3.39 meters per second 

Correct Response: C. Define the potential energy at the lowest point of the path of the swing to be zero. At this point the swing attains its maximum speed and its total mechanical energy is kinetic energy only. When the swing is at its maximum height, h sub max left paren theta equals 45 degrees right paren, the total energy is potential energy only. By the principle of the conservation of mechanical energy, M G H sub max equals 1 half m v squared sub max or V sub max equals the square root of 2 G H sub max Using triangle trigonometry, h sub max equals 2 m minus 2 cosine 45 degrees m equals .586 meters Using g equals 9.8 meters per second squared and substituting these values into the expression above, results in v sub max equals 3.39 meters per second

---

Competency 0007 
Apply knowledge of electric charge and the electric field.

5.  start bold Use the diagram below to answer the question that follows. end bold 

   

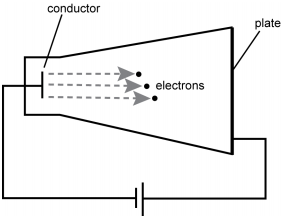
The diagram shows a conical electron gun, with a conductor at the narrow end and a plate at the wide end. Between the conductor and the plate are dashed horizontal arrows labeled electrons. A wire connects the conductor to the plate outside the electron gun, with a voltage source in line.

The diagram above shows an electron gun. Electrons of mass m and charge q are ejected from a hot conductor. The electrons are attracted to a plate that is at a potential V with respect to the conductor. Assuming that the electrons start from rest, which of the following equations gives the speed (nonrelativistic) at which the electrons strike the plate?

1. 
2. 
3. 
4. 

Answer

Correct Response: A.

When a stationary electron leaves the conductor it is accelerated towards the plate by an electric field. The work done on the electron by the electric field is given by the product of charge of the electron, q, and the potential difference between the conductor and the plate, V. The law of conservation of energy states that the work done by the field is equal to the change in kinetic energy of the electron, or qV = ¹/₂mv².  q V equals 1 half m v squared.  Solving this equation for v shows that v = v equals the square root of 2 q V over m.

Correct Response: A. When a stationary electron leaves the conductor it is accelerated towards the plate by an electric field. The work done on the electron by the electric field is given by the product of charge of the electron, Q, and the potential difference between the conductor and the plate, V. The law of conservation of energy states that the work done by the field is equal to the change in kinetic energy of the electron, or q V equals 1 half m v squared. Solving this equation for V shows that v equals the square root of 2 q V over m.

---

Competency 0008 
Analyze characteristics of the magnetic field, magnetic interactions with charges, and principles of electromagnetic induction.

6.  start bold Use the diagram below to answer the question that follows. end bold 

   

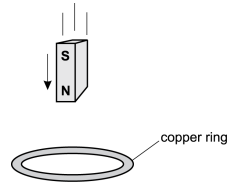
The diagram shows a bar magnet, with the north end down and the south end up, falling through the center of a copper ring.

A magnet is passed through a copper ring at a constant speed as shown above. If current in the counterclockwise direction is considered positive, which of the following graphs could represent the current (I) in the ring as a function of time (t)?

Each response is a graph with the horizontal axis labeled t and the vertical axis labeled I.

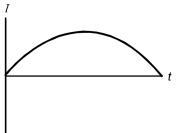1. The data curve is the upper half of a sinusoidal wave, extending the length of the horizontal axis.
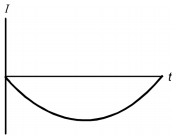2. The data curve is the lower half of a sinusoidal wave, extending the length of the horizontal axis.
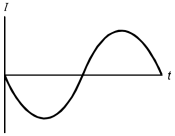3. The data curve is a sinusoidal wave, starting downward, extending the length of the horizontal axis.
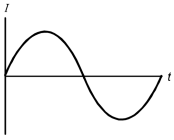4. The data curve is a sinusoidal wave, starting upward, extending the length of the horizontal axis.

Answer

Correct Response: D.

According to Lenz's law, the current induced in the ring will be in a direction to oppose the change in magnetic flux through the coil. As the north pole of the magnet approaches the ring, the current will be induced in a direction to create a magnetic field in the ring such that the north pole of the field due to the current repels the north pole of the bar magnet. It follows from the right-hand rule that the current will flow in the counter-clockwise, or positive, direction. After the magnet has passed halfway through the loop, the current in the loop will reverse direction to produce a magnetic field with a north pole pointing down to attract the receding south pole of the bar magnet. The current will therefore be negative as the bar recedes from the copper loop.

Correct Response: D. According to Lenz's law, the current induced in the ring will be in a direction to oppose the change in magnetic flux through the coil. As the north pole of the magnet approaches the ring, the current will be induced in a direction to create a magnetic field in the ring such that the north pole of the field due to the current repels the north pole of the bar magnet. It follows from the right-hand rule that the current will flow in the counter-clockwise, or positive, direction. After the magnet has passed halfway through the loop, the current in the loop will reverse direction to produce a magnetic field with a north pole pointing down to attract the receding south pole of the bar magnet. The current will therefore be negative as the bar recedes from the copper loop.

---

Competency 0009 
Apply knowledge of electric circuits.

7.  start bold Use the circuit diagram below to answer the question that follows. end bold 

   

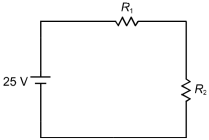
The circuit is a rectangle with a 25 V source on the left side, a resister labeled R sub 1 on the top, and a resistor labeled R sub 2 on the right side.

In the DC circuit above, R₁ = 5 Ω  R sub 1 equals 5 ohm  and R₂ = 10 Ω.  R sub 2 equals 10 ohm  Which of the following changes to the circuit would result in a current flow of 2 A through R₂?  R sub 2 

1. connecting a 5 Ω resistor in series with R₁ and R₂  connecting a 5 ohm resister in series with R sub 1 and R sub 2 
2. connecting a 5 Ω resistor in parallel with R₁  connecting a 5 ohm resister in parallel with R sub 1 
3. connecting a 5 Ω resistor in parallel with R₂  connecting a 5 ohm resister in parallel with R sub 2 
4. connecting a 10 Ω resistor in parallel with R₁  connecting a 10 ohm resister in parallel with R sub 1 

Answer

Correct Response: B.

The equivalent resistance R_e  R sub e  of two resistors R_a  R sub a  and R_b  R sub b  in parallel is given by ¹/_Re = ¹/_Ra + ¹/_Rb. 1 over R sub e equals 1 over R sub a plus 1 over R sub b. If a 5 Ω resistor is connected in parallel with R₁,  if a 5 omega resistor is connected in parallel with r sub 1  ¹/_Re = ²/_5^W 1 over R sub e equals 2 over 5 sup W or R_e = 2.5 Ω.  R sub e equals 2.5 ohm  Since R_e  R sub e  and R₂  R sub 2  are in series, the total resistance of the circuit is R_e + R₂ = 12.5 Ω.  R sub e plus R sub 2 equals 12.5 ohm  Using Ohm's law and solving for I results in I = ^V/_R = 2 amperes  I equals V over R equals 2 amperes  of current flowing through R₂.  R sub 2 

Correct Response: B. The equivalent resistance R sub e of two resistors R sub a and R sub b in parallel is given by 1 over R sub e equals 1 over R sub a plus 1 over R sub b. If a 5 ohm resistor is connected in parallel with r sub 1, 1 over R sub e equals 2 over 5 sup W, or R sub e equals 2.5 ohm. Since R sub e and R sub 2 are in series, the total resistance of the circuit is R sub e plus R sub 2 equals 12.5 ohm. Using Ohm's law and solving for I results in I equals V over R equals 2 amperes of current flowing through R sub 2.

---

Competency 0012 
Apply knowledge of light and optics.

8.  start bold Use the diagram below to answer the question that follows. end bold 

   

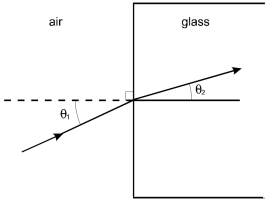
The diagram shows a rectangular mass of glass, with air outside the glass to the left. The horizontal centerline is marked, and is indicated as being at a right angle to the vertical surface of the glass. A ray of light approaches the glass from below on the left at angle theta sub 1. It enters the glass at the centerline and continues at angle theta sub 2, which appears to be less than angle theta sub 1.

The diagram above shows a ray of light passing from air (speed of light in air = v₁ speed of light in air equals v sub 1 ) to glass (speed of light in glass = v₂ speed of light in glass equals v sub 2 ) with an angle of incidence of θ₁. theta sub 1  Which of the following expressions represents sin θ₂? sine theta sub 2? 

1. ^V₁/_V2 (sin θ₁) V sub 1 over V sub 2 left paren sine theta sub 1 right paren
2. ^V₁/_V2 (cos θ₁) V sub 1 over V sub 2 left paren cosine theta sub 1 right paren
3. ^V₂/_V1 (sin θ₁) V sub 2 over V sub 1 left paren sine theta sub 1 right paren
4. ^V₂/_V1 (cos θ₁) V sub 2 over V sub 1 left paren cosine theta sub 1 right paren

Answer

Correct Response: C.

From Snell's law, n₁sinθ₁ = n₂sinθ₂,  n sub 1 sine theta sub 1 equals n sub 2 sin theta sub 2  where θ₁  theta sub 1  is the angle of incidence, θ₂  theta sub 2  is the angle of refraction, n₁  n sub 1  is the index of refraction for air, and n₂  n sub 2  is the index of refraction for glass. Therefore, sinθ₂ = ⁿ¹/_n2sinθ₁.  sin theta sub 2 equals n sup 1 over n sub 2 sin theta sub 1.  The index of refraction is related to v, the speed of light in the given material, by n = ^c/_v, by n equals c over v where c is the speed of light in a vacuum. Substituting this result for n₁ n sub 1 and n₂ results in sin θ₂ = ^V₂/_V1sinθ₁. n sub 2 results in sine theta sub 2 equals V sub 2 over V sub 1 sine theta sub 1

Correct Response: C. From Snell's law, n sub 1 sine theta sub 1 equals n sub 2 sine theta sub 2 where theta sub 1 is the angle of incidence, theta sub 2 is the angle of refraction, n sub 1 is the index of refraction for air, and n sub 2 is the index of refraction for glass. Therefore, sine theta sub 2 equals n sup 1 over n sub 2 sine theta sub 1. The index of refraction is related to v, the speed of light in the given material, by n equals c over v where c is the speed of light in a vacuum. Substituting this result for n sub 1 and n sub 2 results in sine theta sub 2 equals V sub 2 over V sub 1 sine theta sub 1

---

Competency 0013 
Apply knowledge of kinetic theory and the laws of thermodynamics.

9.  start bold Use the graph below to answer the question that follows. end bold 

   

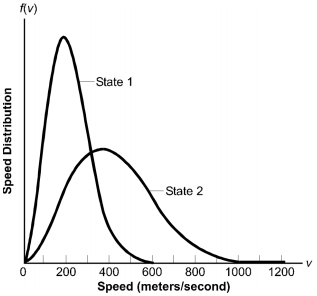
The horizontal axis of the graph is labeled Speed in meters per second, with values marked from 0 to 1200 in increments of 200. It is also labeled v. The vertical axis is labeled Speed Distribution, with no values marked. It is also labeled f of v. There are 2 data curves, labeled State 1 and State 2. The State 1 curve starts at the origin, rises steeply, makes a smooth turn at the peak around a v value of about 200, falls steeply, then levels off gradually to end at a v value of about 600. The State 2 curve is a similar shape, but half as high and twice as wide, rising to its peak around a v value of about 400 and ending at a v value of about 1200.

An ideal gas at a constant volume is taken from state 1 to state 2. The graph above shows the speed distribution curves f (v) for the gas in each of the states. Which of the following statements best describes how the gas was taken from State 1 to State 2?

1. Thermal energy was added to the gas, causing an increase in the temperature of the gas.
2. Work was done on the gas, causing an increase in the temperature of the gas.
3. Thermal energy was removed from the gas, causing a decrease in the temperature of the gas.
4. Work was done by the gas, causing a decrease in the temperature of the gas.

Answer

Correct Response: A.

From the first law of thermodynamics, ΔQ = dE − W = CΔT − pdV.  delta Q equals d E minus W equals C delta T minus P D V  Since V is constant, dV = 0,  d V equals 0  so no work was done by or on the gas. From the speed distribution curves, the average speed (v_a v sub a ) of the molecules is greater in State 2 than in State 1. Since T ∝¹/₂mv_a²,  T is inversely proportional to 1 half m v sub a squared  the temperature of the gas is greater in State 2. Thus, both ΔT  delta T  and ΔQ  delta Q  are positive.

Correct Response: A. From the first law of thermodynamics, delta Q equals d E minus W equals C delta T minus P D V. Since V is constant, d V equals 0 so no work was done by or on the gas. From the speed distribution curves, the average speed, left paren, v sub a, right paren, of the molecules is greater in State 2 than in State 1. Since T is inversely proportional to 1 half m v sub a squared the temperature of the gas is greater in State 2. Thus, both delta T and delta Q are positive.

---

Competency 0015 
Apply knowledge of quantum theory of light and matter.

10. Which of the following best explains why macroscopic objects have properties that are more particle-like than wavelike?

1. The wavelength of a macroscopic object is too small for the object to be diffracted.
2. The laws of quantum mechanics are valid only for quantities of the order of Planck's constant.
3. The uncertainty principle implies a small value for the position and momentum of macroscopic objects.
4. The wave function for a macroscopic object has both a real and an imaginary part.

Answer

Correct Response: A.

Wave-like properties of objects are observed when an object undergoes diffraction. Diffraction requires scattering from an obstacle or aperture of approximately the same size as the wavelength of the incident object. Since pλ = h, and h = 6.63 × 10^–34 J•s, using p = mv = (1 kg)(1 m/s) for a typical macroscopic object results in a wavelength of the order of 10^–33 m. This wavelength is significantly smaller than the size of the nucleus of an atom (10^–15 m).

Correct Response: A. Wave-like properties of objects are observed when an object undergoes diffraction. Diffraction requires scattering from an obstacle or aperture of approximately the same size as the wavelength of the incident object. Since p lambda equals h, and h equals 6.63 times 10 to negative 34 joule seconds, using p equals mv equals left paren 1 kilogram right paren left paren 1 meter per second right paren for a typical macroscopic object results in a wavelength of the order of 10 to negative 33 meters. This wavelength is significantly smaller than the size of the nucleus of an atom left paren 10 to negative 15 meters right paren.

---

Copyright © 2015 by the Office of Educational Quality and Accountability and Pearson Education, Inc. or its affiliate(s).
All rights reserved.
Pearson, 300 Venture Way, Hadley, MA 01035